http://www.ghtc.usp.br/ram-r67.htm
 

COMO DISTORCER A FÍSICA: CONSIDERAÇÕES SOBRE UM EXEMPLO DE DIVULGAÇÃO CIENTÍFICA. 2 – FÍSICA MODERNA Roberto de Andrade Martins

Um artigo anterior já apresentou uma análise crítica da primeira metade da obra A dança do universo, de Marcelo Gleiser, como um exemplo de trabalho de divulgação científica que apresenta grandes limitações, sob o ponto de vista conceitual. Neste artigo, vamos discutir alguns aspectos da segunda metade do livro, dedicada à física moderna. Veremos que também aqui a obra em discussão mostra-se repleta de equívocos, muitas vezes em pontos conceituais centrais da física. Como no artigo anterior, vamos procurar evitar comentários sobre os aspectos de história da ciência ou de epistemologia, concentrando nossa atenção em questões científicas e didáticas.
 

Este artigo vai apresentar uma discussão crítica baseada na segunda edição do livro. Para poder acompanhar a análise aqui apresentada, é conveniente ter à mão o próprio livro. A primeira edição continha alguns outros problemas adicionais, que foram corrigidos e que não serão apontados aqui. No entanto, quem dispuser apenas da primeira edição, poderá encontrar as falhas aqui discutidas, nas mesmas páginas indicadas.

Como já foi dito no artigo anterior, a escolha desta obra em particular para análise não significa que eu a considere a pior já escrita, nem que tenha algum problema pessoal com o autor (que não conheço). Creio que o tipo de análise crítica aqui apresentada pode ser útil aos estudantes e educadores, e servir também de alerta a autores e editoras, para que procurem ser mais cuidadosos em trabalhos desse tipo.

Alguns pontos serão indicados de modo muito resumido, para poupar espaço. Teria sido possível explicar melhor cada um deles, mas espero que os leitores possam completar por si próprios a análise apresentada.

II – Teoria da relatividade especial

Ao descrever a origem da teoria da relatividade, o livro A dança do universo apresenta uma descrição histórica pouco fiel, que não será discutida aqui, a não ser em alguns pontos fundamentais, que afetam a compreensão da própria natureza científica da teoria da relatividade. Em primeiro lugar, quanto aos experimentos de Michelson:

Por outro lado, nem o experimento de Michelson e Morley nem qualquer outro experimento permitem estabelecer a não existência do éter. Ao contrário do que popularmente se divulga, não existe nenhuma prova de que o éter não existe: simplesmente a teoria da relatividade (no sentido de Einstein) adotou o princípio epistemológico de que não se deve utilizar na física entes que não sejam observáveis, e assim rejeitou o éter, porque ele não havia sido detectado em certos experimentos¹. Outras pessoas aceitaram exatamente os mesmos experimentos, mas adotaram uma interpretação diferente (aceitando o éter), por utilizarem princípios epistemológicos diferentes (por exemplo, Poincaré).
 

1  Na verdade, havia experimentos realizados no século XIX, por Fizeau e por Ångström, que aparentemente haviam medido a velocidade da Terra em relação ao éter. Ver MARTINS 1986a.

O éter não era uma suposição tola: na verdade, tolice é falar-se sobre um espaço totalmente vazio (MARTINS 1993). No final do século XIX e início do século XX, o éter preenchia o papel de proporcionar uma explicação causal para alguns fenômenos físicos (por exemplo, propagação da luz e dos campos eletromagnéticos), e na versão de Lorentz e Poincaré permitia uma explicação causal de fenômenos como a contração dos corpos em movimento (essa contração seria causada por uma variação das forças eletromagnéticas entre as partículas do corpo, que, por sua vez, seria causada pelo movimento através do éter). O aumento de massa de um elétron era explicado a partir do momento acumulado ao redor do mesmo, no éter, pelos campos eletromagnéticos. Na versão de Einstein, a teoria da relatividade prevê os efeitos, mas não se preocupa em apresentar uma explicação causal dos fenômenos (MARTINS 1981).

Não se pode, portanto, afirmar que "Michelson continuou a acreditar na existência do éter até o fim de sua vida, mesmo após a teoria da relatividade de Einstein ter elegantemente demonstrado que esse meio era completamente desnecessário" (GLEISER, A dança do universo, p. 254). A teoria de Einstein permitia fazer deduções sem fazer referência ao éter, mas isso não indica que o éter era completamente desnecessário. É bem sabido, aliás, que na década de 1920 Einstein voltou a aceitar a existência do éter.

Mais adiante, o livro afirma de modo ainda mais forte:

O livro apresenta a proposta da contração por Lorentz e Fitzgerald de um modo ridículo:

Voltando à seqüência do livro:

O livro procura justificar a constância da velocidade da luz a partir da teoria eletromagnética:

O livro apresenta de um modo confuso o princípio da relatividade:

O conceito de velocidade limite de processos causais não é uma das suposições básicas da teoria – é uma conseqüência da teoria, obtida quando se adiciona o princípio de antecedência das causas – ou seja, que uma causa nunca ocorre depois do seu efeito (MARTINS 1986b).

III – Dedução dos fenômenos relativísticos

Muitos autores já se esforçaram, ao longo das décadas, para apresentar deduções extremamente simples das transformações de espaço e tempo da relatividade especial. O tipo de dedução que me parece mais simples e conceitualmente correto é o que aparece (entre outros lugares) nas conferências de Feynman, e que se baseia em relógios de luz (FEYNMAN et al., The Feynman lectures on physics, vol. 1, cap. 15). O livro A dança do universo procurou inovar essas deduções, mas cometeu equívocos graves.

Quando o livro procura justificar a dilatação temporal e a contração dos comprimentos (GLEISER, A dança do universo, p. 269 e seguintes), há um problema físico não muito óbvio, mas importante. As transformações usuais entre períodos de relógios, do tipo T = T₀.(1–v²/c²)^–1/2 são válidas se e somente se o período T₀ é um período próprio para um dos referenciais. Ou seja, ele deve ser o intervalo de tempo entre dois eventos que ocorrem na mesma posição para um dos dois referenciais. Isso pode ser confirmado notando-se que a fórmula pode ser deduzida da quarta transformação de Lorentz se e somente se Dx for nulo:

Outro ponto é que o livro introduz um som, na análise: o observador ouve os "tiques" e "taques". Mas o som demora um certo tempo (muito maior do que o período) para se propagar até o observador, e isso teria que ser levado em conta, o que complicaria extremamente a análise quantitativa, se ela fosse feita. Qualitativamente, isso complica muito a compreensão do fenômeno estudado. É muito mais fácil tratar de dois eventos que ocorram no mesmo ponto (duas reflexões sucessivas da luz no espelho superior ou no inferior), o que elimina qualquer necessidade de introduzir o som ou outro sinal difícil de ser analisado.

No primeiro uso que o livro A dança do universo faz do relógio de luz (dilatação dos períodos dos relógios), o erro conceitual não introduziria nenhum problema em uma dedução quantitativa: pode-se chegar à fórmula correta (basicamente porque, embora o "tique" e o "taque" ocorram em dois pontos diferentes, o Dx é igual a zero). Mas na segunda análise, em que o relógio é colocado "deitado" (na direção do movimento), o "tique" e o "taque" ocorrem em posições diferentes ao longo do eixo do movimento, e existe um Dx diferente de zero que introduz um grande problema. O raciocínio apresentado para justificar a contração dos comprimentos está errado:

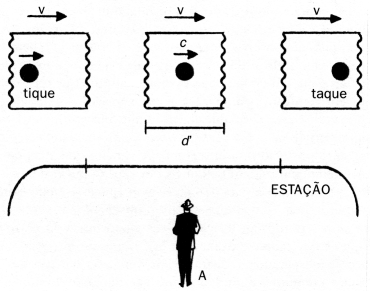
Esse raciocínio está errado. Se ele for utilizado para deduzir quantitativamente a contração dos comprimentos, a conclusão será que o comprimento do relógio se contrairia de acordo com a relação L = L₀.(1–v²/c²) e não de acordo com a fórmula correta, L = L₀.(1–v²/c²)^1/2 (deixo a dedução para o leitor). Além disso (e muito pior do que isso!), se o relógio do livro for invertido, de tal modo que a luz caminhe para a esquerda ( ¬ ) entre o "tique" e o "taque", a conclusão teria que ser oposta, ou seja, adaptando-se o texto anteriormente citado do livro:

Na dedução correta, utiliza-se luz que caminha nos dois sentidos, indo e voltando. O tempo de ida é L/(c–v) e o tempo de volta é L/(c+v); o tempo total é T=2Lc/(c²–v²) = (2L/c)/(1–v²/c²). Como o período próprio é T₀=2L₀/c, e como a transformação do período é T=T₀.(1–v²/c²)^–1/2, deduz-se daí a relação correta para a contração do comprimento.

IV – Outros aspectos da relatividade

Ao tentar exemplificar os efeitos relativísticos, o livro menciona os raios cósmicos, que são assim descritos:

O livro contém muitas frases de efeito, como a seguinte:

Há uma relação entre massa e energia, de tal modo que quase sempre elas são proporcionais. As exceções são os casos em que um sistema extenso está submetido a pressões e tensões externas, e o caso da energia potencial eletromagnética, à qual não se pode associar uma massa (ver MARTINS 1989). Por exemplo: um elétron dentro de um Van de Graaf pode ter uma energia potencial positiva ou negativa muitas vezes superior à sua energia de repouso, mas isso não afeta seu comportamento dinâmico, ou seja, não afeta sua massa.

A relação entre massa e velocidade não foi deduzida da relação E = mc² – ela é mais antiga, e vem do estudo do momento do campo eletromagnético em torno de uma carga em movimento. Antes de 1905, a relação entre massa e velocidade já havia sido deduzida e testada experimentalmente (ver MARTINS 1989).

V – Teoria quântica

O capítulo seguinte do livro introduz a problemática da teoria quântica com uma discussão sobre a cor da luz emitida por um corpo aquecido:

A segunda citação diz que "a barra metálica se tornaria cada vez mais amarelada, até que, a temperaturas extremamente altas, ela emitiria uma luz azulada", o que não está correto. A barra se tornaria mais amarelada, depois branca, e depois (se não derretesse) ficaria azulada. Na verdade, nenhum sólido conhecido pode atingir temperaturas tão altas (e nenhum forno, também).

A física clássica explicava o deslocamento das freqüências luminosas em função da temperatura, mostrando que a freqüência do máximo de intensidade devia ser proporcional à temperatura absoluta. A explicação não dependia do eletromagnetismo – era puramente termodinâmica.

A explicação dada no livro ("quanto mais quente a barra, mais rapidamente as cargas vibram") está incorreta, sob o ponto de vista da física clássica. Admitindo-se cargas elétricas que oscilam (como foi feito primeiramente por Lorentz e, depois, por Planck), a freqüência de oscilação seria uma característica fixa de cada oscilador (demonstra-se em qualquer livro de mecânica que a freqüência de um oscilador harmônico independe de sua energia), e não poderia aumentar com a temperatura. O que mudaria com a temperatura seria a amplitude das vibrações, e a distribuição de energia pelos osciladores.

Errado. Um absorvedor ideal é também um emissor ideal, conforme provado por Kirchhoff através de argumentos termodinâmicos. Um pequeno orifício conectado a uma cavidade aquecida emite mais radiação do que qualquer tipo de superfície, à mesma temperatura.

Ao descrever a descoberta dos raios X, o livro apresenta uma figura errônea, sob os pontos de vista histórico e físico (GLEISER, A dança do universo, p. 289, fig. 8.3).

Nos tubos de raios catódicos utilizados inicialmente por Röntgen e outros pesquisadores para produzir raios X, o ânodo não ficava na frente do cátodo, e sim ao lado. O feixe de raios catódicos que saia do cátodo caminhava em linha reta e atingia o vidro do tubo. O desenho apresenta um esquema de uma bateria ligada ao tubo de descarga, produzindo os raios X. Isso é impossível, pois somente com altas voltagens (milhares de volts) é possível produzir-se raios X. Por isso, Röntgen e os pesquisadores da época utilizavam bobinas de indução, capazes de produzir uma diferença de potencial de dezenas (às vezes centenas) de milhares de volts.

A descrição da descoberta da radioatividade apresenta também inúmeros problemas.

Passando à teoria quântica, aparecem conceitos não muito corretos, como por exemplo:

Referindo-se à teoria do átomo de Bohr, o livro comenta:

Em relação à interpretação da teoria quântica, o livro afirma:

Dentro da teoria quântica, ao contrário do que afirma o livro, podemos determinar a posição de um elétron, por exemplo, com a precisão que quisermos. O que não é possível é determinar ao mesmo tempo uma coordenada e o momento conjugado.

VI – Relatividade geral e princípio de equivalência

A apresentação que o livro faz da relatividade geral também introduz noções problemáticas.

Há efeitos gravitacionais, previstos pela relatividade geral, que são muito pequenos e difíceis de se detectar sem se utilizar campos mais fortes, como os das estrelas (por exemplo, deflexão da luz). No entanto, mesmo no campo terrestre, é possível detectar-se, por exemplo, o efeito do desvio para o vermelho (em experimentos de laboratório, sem observar estrelas), e portanto, ao contrário do que afirma o livro, os efeitos sobre o fluxo do tempo não são desprezíveis.

Ao tentar introduzir a necessidade de uma generalização da teoria da relatividade especial no tratamento da gravidade, o livro afirma:

O princípio de equivalência da relatividade geral é usualmente introduzido por meio de exemplos de um elevador acelerado ou em queda livre, mas o livro em discussão apresenta várias idéias incorretas, ao falar sobre isso:

O mesmo erro aparece depois:

A frase "objetos que se movem com velocidade constante no elevador continuarão a mover-se com velocidade constante se o elevador estiver em queda livre" parece não ter sentido. Os objetos já estavam se movendo com velocidade constante antes que o elevador estivesse em queda livre? Eles não sofriam a aceleração da gravidade?

"Em outras palavras: dentro do elevador em queda livre, os princípios da relatividade especial são perfeitamente válidos" – isso não é correto. Trata-se de outro exemplo em que o livro afirma uma conexão lógica inexistente. Aquilo que precede essa frase não permite concluir que o princípio da relatividade e o princípio da constância da velocidade da luz são válidos em relação ao referencial do elevador (e que não são válidos em relação a outro referencial). A única coisa que foi mostrada foi que os corpos, em relação ao referencial do elevador em queda livre, parecem não estar sujeitos a forças externas, e que se movem de modo aparentemente inercial. Como o livro não esclareceu o conceito de referencial inercial, não dá para conectar isso com a relatividade especial.

Há um outro ponto problemático. Neste ponto do livro, após falar sobre a teoria quântica, o autor já não deveria mais associar emissão de radiação eletromagnética com vibração de cargas elétricas. No entanto, o livro continua a utilizar esse modelo clássico:

VI – Espaços não euclidianos

O conceito de espaço-tempo curvo é fundamental na teoria da relatividade geral, mas desde sua introdução o livro se enreda em dificuldades:

A mesma afirmação incorreta de que tudo se reduz a utilizar espaços curvos reaparece em vários pontos (ver, por exemplo, pág. 332).

Muito bem, precisamos pressionar a superfície elástica para produzir uma deformação. Vamos empurrar a bola, e deformar a cama elástica. Teremos agora uma boa analogia? Não. Na teoria da relatividade geral, uma fonte de campo deforma o espaço-tempo, mas isso não é devido a uma força exercida pela fonte do campo (na verdade, queremos explicar a força gravitacional, e por isso utilizamos uma coisa que não é uma força).

A analogia da cama elástica só parece funcionar porque nela interferem, duas vezes, a própria força gravitacional (para deformar a superfície e para mover as bolinhas de gude). No entanto, já que se quer explicar exatamente a força gravitacional, é inválido utilizar como modelo um fenômeno que só ocorre por causa da própria gravidade.

Na relatividade geral, o movimento de uma partícula no campo gravitacional é descrito sem se falar em forças, introduzindo um espaço-tempo com métrica curva, e calculando-se as geodésicas nesse espaço-tempo. Em um sentido matemático bem preciso, as partículas descrevem "retas" (geodésicas) do espaço-tempo, mas não "retas" (geodésicas) do espaço. A analogia da cama elástica não capta nenhum desses aspectos – desvia apenas a atenção do leitor, que pensa ter entendido alguma coisa, mas que não pode captar pela analogia nada de correto sobre a relatividade geral.

Também está errado dizer que "Perto da massa, as bolas de gude seguirão órbitas circulares ou elípticas". A única possibilidade de surgirem órbitas elípticas (desprezando-se o atrito) será se a superfície tiver exatamente uma forma adequada para simular uma força inversamente proporcional ao quadrado da distância. Suponhamos que a superfície seja descrita em função de r, f e z (coordenadas cilíndricas). A projeção horizontal do movimento das bolas de gude poderá ser elíptica apenas se valer a relação

sin 2a = k/r²

onde a = arctan (dz/dr). Isso exige, portanto, condições extremamente especiais da forma da superfície elástica. Aliás, se a cama elástica for quadrada (como no caso do livro), isso nunca será possível.

Na página 332, encontramos uma referência à nota (9), que diz:

Ao descrever o desenvolvimento das geometrias não-euclidianas, o livro comenta:

O conceito de curvatura gaussiana está associado à existência de um excesso (ou defeito) angular. Em um triângulo, o excesso angular é a diferença entre a soma dos ângulos internos do triângulo e 180°. Em um quadrado, o excesso angular é a diferença entre a soma dos seus ângulos internos e 360°. A curvatura gaussiana média de uma região (por exemplo, triangular ou quadrada) é dada pela razão entre a diferença angular e a área da região. Esse conceito pouco óbvio não foi passado no livro, e no entanto fica-se o tempo todo falando em "curvatura", como se fosse um conceito intuitivo.

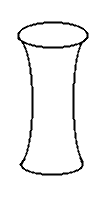
A curvatura na região central será negativa, mas é possível caminhar na mesma direção e voltar ao ponto de partida (dependendo da direção).

Resumindo: há grandes problemas na conceituação geométrica apresentada, porque o livro fica passando de um conceito para outro, como se fossem equivalentes, quando na verdade são conceitos diferentes e – em grande parte – independentes.

VII – Cosmologia relativística

Como o livro tem por objetivo central discutir modelos cosmológicos, esperaríamos que, pelo menos nessa parte, o texto fosse rigoroso e correto. Mas isso não ocorre em muitos pontos.

Ao descrever o modo de estimar as distâncias de estrelas e galáxias, o livro afirma:

Por outro lado, "luminosidade intrínseca" não é a intensidade a uma distância fixa, e sim a potência luminosa total emitida pela fonte. Se chamarmos de S o fluxo luminoso (medido em J.m^–2.s^–1) recebido a uma distância d de uma fonte isotrópica, a luminosidade L da fonte é L=4pd²S (medido em J.s^–1)

No texto, a apresentação da lei de Hubble está boa, mas no Glossário aparece:

Além disso, o final da frase está errado: as galáxias não iriam se aproximando indefinidamente, porque elas e as estrelas iriam se desfazendo. O que se poderia afirmar é que, se a expansão não partiu de uma certa densidade máxima, e se a matéria se conserva, a matéria estaria agrupada em uma região muito pequena do espaço.

VIII – Física nuclear e partículas

Para explicar a energia liberada pelas estrelas, o livro introduz noções de física nuclear:

Ao representar por figuras a estrutura atômica (GLEISER, A dança do universo, p. 375, fig. 10.1) o livro apresenta uma visão há muito ultrapassada, como se os elétrons e núcleons fossem bolinhas, e os elétrons tivessem órbitas bem definidas em torno do núcleo (mais adiante, a fig. 10.2, pág. 383, continua representando prótons e até mesmo quarks como "bolinhas"). Por outro lado, a união de um próton e um nêutron não deveria ser chamada de "deutério" e sim de "dêuteron", e assim por diante. "Deutério" se aplica a um tipo de átomo, e não ao núcleo desse átomo.

Ao explicar a fusão nuclear, o livro descreve o processo de formação do hélio da seguinte forma:

H² (dêuteron) + H³ (trítion) ® He⁴ (núcleo de hélio) + n + 17.6 MeV

No interior das estrelas, a reação que ocorre também não é nenhuma das indicadas no livro, e sim a seguinte:

He³ (núcleo de hélio) + He³ (núcleo de hélio) ® He⁴ (núcleo de hélio) + p + p

Quando se produz uma fusão de dois dêuterons, a probabilidade de obter-se um núcleo de hélio H⁴ é quase nula. Obtém-se H³ e emissão de um próton ou nêutron.

Mesmo para elementos abaixo do ferro, dependendo dos isótopos considerados, a fusão só é possível com fornecimento de energia.

a) Questões sobre origens: De onde surgiram as montanhas? De onde surgiu a água? De onde surgiram as rochas? De onde surgiu o sabor salgado do mar?

b) Questões sobre causas: Por que o céu é azul? Por que as nuvens não caem? Por que a duração dos dias e das noites varia ao longo do ano? Por que a água fica dura quando esfria?

c) Questões sobre a natureza das coisas: O que são os raios? O que são as estrelas? O que é o ar?

d) Questões sobre constituintes: Como é o interior da Terra? Como é o interior dos vulcões? Como é o interior das pedras? Qual a diferença entre a água e o ar?

IX – Comentários finais

A física moderna, por estar mais distante de nossas concepções intuitivas sobre o universo, é mais difícil de ser compreendida e explicada. Não é impossível, no entanto, descrever os resultados conceituais mais importantes da física moderna em linguagem qualitativa. A revista Scientific American, para citar apenas uma fonte, é um excelente exemplo de divulgação científica da física moderna, com artigos bem escritos, interessantes e ao mesmo tempo corretos.

Muitas vezes, as pessoas que se dedicam à divulgação científica transmitem informações errôneas, por vários motivos. Um primeiro motivo é que algumas vezes escrevem sobre algo que escapa ao seu domínio científico – por exemplo, uma pessoa com formação jornalística escrevendo sobre um tema altamente técnico, ou um cientista com treino em uma área específica escrevendo sobre outra área. Um segundo motivo que leva a conteúdos incorretos é a tentativa bem intencionada de tornar as informações compreensíveis, através de comparações e analogias, que infelizmente podem levar a deformações infelizes do conteúdo científico.

Há algumas condições básicas para se escrever um livro de divulgação sobre física moderna: ter uma excelente compreensão conceitual do assunto, percebendo as condições de validade e os limites de cada idéia, suas semelhanças e diferenças com idéias da física clássica; dispor de um bom estoque de comparações, analogias e ilustrações, utilizando-as cautelosamente e alertando o leitor para os pontos em que as semelhanças deixam de existir; e ser capaz de escrever com um estilo que capte a atenção do leitor. É preciso saber simplificar as idéias mais complicadas, mas sem falseá-las, pois um erro, depois de assimilado, dificilmente é erradicado.

Referências bibliográficas

1. FEYNMAN, Richard P., LEIGHTON, Robert B. & SANDS, Matthew. The Feynman lectures on physics. 3 vols. Reading: Addison-Wesley, 1965.
2. GLEISER, Marcelo. A dança do universo. Dos mitos de criação ao big-bang. 2. ed. São Paulo: Companhia das Letras (Editora Schwarcz), 1997.
3. HALIDAY, David, RESNICK, Robert & MERRILL, John. Fundamentos da física. 1 – Mecânica. 2. ed. Rio de Janeiro: Editora LTC, 1993.
4. MARTINS, Roberto de Andrade. Use and violation of operationalism in relativity. Manuscrito 5 (2): 103-15, 1981.
5. MARTINS, Roberto de Andrade. A Popperian evaluation of Einstein's theory-plus-method. Manuscrito 9 (2): 85-113, 1986 (a).
6. MARTINS, Roberto de Andrade. O princípio de antecedência das causas na teoria da relatividade. Anais da ANPOF 1 (1): 51-72, 1986 (b).
7. MARTINS, Roberto de Andrade. A relação massa-energia e energia potencial. Caderno Catarinense de Ensino de Física 6: 52-84, 1989.
8. MARTINS, Roberto de Andrade. Como Becquerel não descobriu a radioatividade. Caderno Catarinense de Ensino de Física 7: 27-45, 1990.
9. MARTINS, Roberto de Andrade. Em busca do nada: considerações sobre os argumentos a favor e contra o vácuo. Trans/Form/Ação 16: 7-27, 1993.
10. MARTINS, Roberto de Andrade. Becquerel and the choice of uranium compounds. Archive for History of Exact Sciences 51 (1): 67-81, 1997.
11. NORTH, John David. The measure of the universe. New York: Dover, 1990.
12. WEINBERG, Steven. Gravitation and cosmology: principles and applications of the general theory of gravitation. New York: John Wiley & Sons, 1972.
13. WHITTAKER, Edmund. A history of the theories of aether and electricity. 2 vols. New York: American Institute of Physics, 1987.